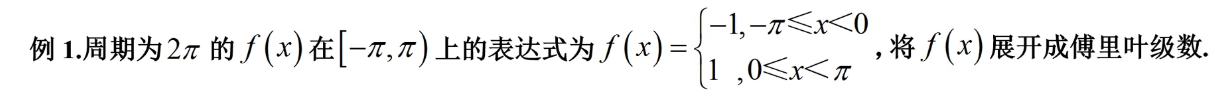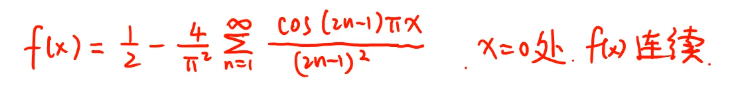傅里叶级数、狄利克雷收敛定理、周期延拓

一、傅里叶级数与幂级数

共同点：都是将一个复杂的量用叠加的简单量来表示。

幂级数展开：简单量——幂函数

傅里叶级数展开：简单量——三角函数

【傅里叶级数主要用于研究周期性的量】

函数能展开成为幂级数的条件是：f(x)任意阶可导。函数能展开称为傅里叶级数的条件就严格多了。

二、 傅里叶级数的收敛性：狄利克雷收敛定理

【狄利克雷收敛定理有2个使用条件】

设函数f(x)是以2l为周期的可积函数，且在[-l，l]上满足2个条件：

①f(x)连续或只有有限个第一类间断点(可去/跳跃) 

②只有有限个极值点

则称f(x)的以2l为周期的傅里叶级数收敛。且

(1)当x是f(x)的连续点时，该级数收敛于  

(2)当x是f(x)的间断点时，该级数收敛于 

(3)当x=±l时(端点处)，该级数收敛于  

即连续的点直接代入，不连续的点取左右极限平均。

三、周期为2l的函数展开为傅里叶级数

1、傅里叶级数的统一形式：

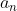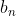2、不同情况下傅里叶系数和的求法：

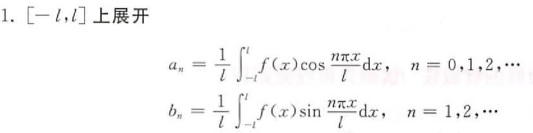
相同点：①积分区间都是：-l→l ②被积函数都是：f(x)·三角函数 ③整体都要乘系数

区别：中只有余弦cos， 中只有正弦sin。中的n从0开始，中的n从1开始。

原理—当f(x)不仅是周期为2l的函数，还是奇/偶函数时：

【奇函数的展开式中只有正弦sin】

，被积函数f(x)·cos 奇×偶=奇→零→积分值=0。

，被积函数f(x)·sin 奇×奇=偶→倍→积分值=

【偶函数的展开式中只有余弦cos】

，被积函数f(x)·cos 偶×偶=偶→倍 →积分值=

，被积函数f(x)·sin 偶×奇=奇→ 零→积分值=0。

注意是在半个周期上展开为正弦or余弦！

补充f(x)在另一半周期[-l,0]上的定义:

要想展开为正弦sin→要使f(x)在[-l, l ]上为奇函数【奇延拓】记忆口诀：正畸(奇)

要想展开为余弦cos→要使f(x)在[-l, l ]上为偶函数【偶延拓】

延拓不改变求an时的积分区间仍为[0, l]半个周期。唯一区别：在使用狄利克雷收敛定理时要在区间[-l, l]上使用。

四、常考题型与经典例题

1、狄利克雷收敛定理

 

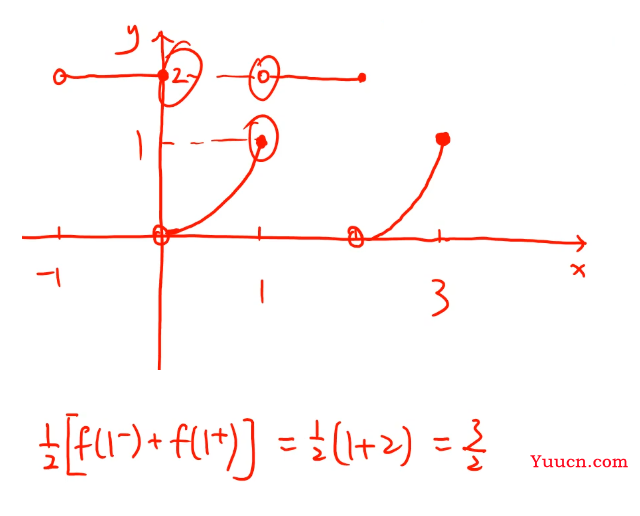
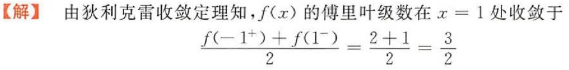
【分析】不用求出傅里叶系数和，直接使用狄利克雷收敛定理——当x是f(x)的间断点时，该级数收敛于 

B

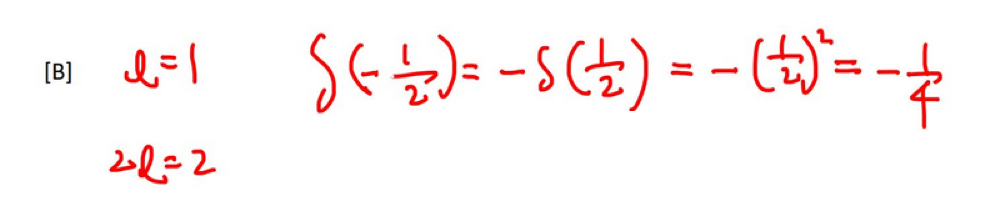
2、将函数展开为傅里叶级数

注：